Apriori Algorithm
13 Apr 20151. 介绍
Apriori算法是一种最有影响的挖掘布尔关联规则频繁项集的算法。其核心是基于两阶段频集思想的递推算法。该关联规则在分类上属于单维、单层、布尔关联规则。在这里,所有支持度大于最小支持度的项集称为频繁项集,简称频集。
1.1 项集
项的集合称为项集。包含k个项的项集称为k-项集。
Candidate-gen(候选项集集合Ck的生成)函数:(F代表频繁项集)
1.2 候选项集
用来获取频繁项集的候选项集,候选项集中满足支持度条件的项集保留,不满足条件的舍弃。
1.3 频繁项集:
集合{computer,ativirus_software}是一个二项集。项集的出项频率是包含项集的事务数,简称为项集的频率,支持度计数或计数。注意,定义项集的支持度有时称为相对支持度,而出现的频率称为绝对支持度。如果项集I的相对支持度满足预定义的最小支持度阈值,则I是频繁项集。
1.4 极大频繁项集
不存在包含当前频繁项集的频繁超集,则当前频繁项集就是极大频繁项集。
1.5 关联规则
关联规则是形如X→Y的蕴涵式,其中且,X和Y分别称为关联规则的先导(antecedent或left-hand-side, LHS)和后继(consequent或right-hand-side, RHS) 。
1.6 支持度
关联规则A->B的支持度support=P(AB),指的是事件A和事件B同时发生的概率。
1.7 可信度
置信度confidence=P(B|A)=P(AB)/P(A),指的是发生事件A的基础上发生事件B的概率。
1.8 举例
在数据挖掘当中,通常用“支持度”(support)和“置性度”(confidence)两个概念来量化事物之间的关联规则。它们分别反映所发现规则的有用性和确定性。
比如: Computer => antivirus_software , 其中 support=2%, confidence=60%
表示的意思是所有的商品交易中有2%的顾客同时买了电脑和杀毒软件,并且购买电脑的顾客中有60%也购买了杀毒软件。在关联规则的挖掘过程中,通常会设定最小支持度阈值和最小置性度阈值,如果某条关联规则满足最小支持度阈值和最小置性度阈值,则认为该规则可以给用户带来感兴趣的信息。
2. 算法
基本过程
-
找出所有的频繁项集:
扫描一遍数据库,得到一阶频繁项;用一阶频繁项构造二阶候选项;扫描数据库对二阶候选项进行计数,删除其中的非频繁项,得到二阶频繁项;然后构造三阶候选项,以此类推,直到无法构造更高阶的候选项,或到达频繁项集的最大长度限制。
-
由频繁项集产生强规则,即产生用户感兴趣的关联规则。
2.1. 产生频繁项集
2.1.1 自连接
若有两个k-1项集,每个项集按照“属性-值”(一般按值)的字母顺序进行排序。
如果两个k-1项集的前k-2个项相同,而最后一个项不同,则证明它们是可连接的,即这个k-1项集可以联姻,即可连接生成k项集。
使如有两个3项集:{a, b, c}{a, b, d},这两个3项集就是可连接的,它们可以连接生成4项集{a, b, c, d}。
又如两个3项集{a, b, c}{a, d, e},这两个3项集显示是不能连接生成3项集的。
2.1.2 剪枝
若一个项集的子集不是频繁项集,则该项集肯定也不是频繁项集。
举一个例子,若存在3项集{a, b, c},如果它的2项子集{a, b}的支持度即同时出现的次数达不到阈值,则{a, b, c}同时出现的次数显然也是达不到阈值的。
因此,若存在一个项集的子集不是频繁项集,那么该项集就应该被舍弃。
2.1.3 举例
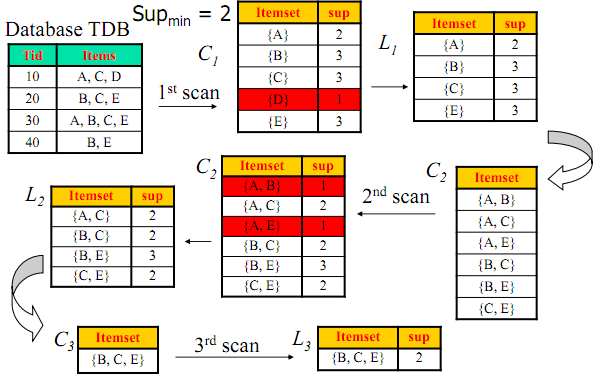
2.2 产生强规则
Confidence(A->B)=support_count(AB)/support_count(A)
关联规则产生步骤如下:
- 对于每个频繁项集l,产生其所有非空真子集;
- 对于每个非空真子集s,如果support_count(l)/support_count(s)>=min_conf,则输出 s->(l-s),其中,min_conf是最小置信度阈值。
例如针对频繁集{a,b,c}。有{a,b},{a,c},{b,c},{a},{b}和{c},对应置信度如下:
a&&b->c confidence=2/4=50%
a&&c->b confidence=2/2=100%
b&&c->a confidence=2/2=100%
a ->b&&c confidence=2/6=33%
b ->a&&c confidence=2/7=29%
c ->a&&b confidence=2/2=100%
如果最小可信度=70%,则强规则有a&&c->b,b&&c->a,c->a&&b。
3 实现
https://github.com/Flowerowl/Apriori
参考:
- http://blog.csdn.net/qustdjx/article/details/12770883
- http://blog.csdn.net/luowen3405/article/details/6318931
- http://blog.csdn.net/mananbao/article/details/7817419
- http://blog.sina.com.cn/s/blog_6fb7db430100vdcf.html
- http://www.tanglei.name/apriori-algorithm-in-python/
- http://blog.sina.com.cn/s/blog_6a17628d0100v83b.html
- http://baike.baidu.com/link?url=UnukpqvaVU41tCDjQpdfPk5di5rlggCviZOXPPraGD_U4tnsuJ-jCc3QsC5p6XLBM-r_lVu1HaBWGP8PC-0OFq