Brief introduction to tensorflow

09 Nov 2018

1. 关于Tensorflow

TensorFlow 是一个采用数据流图（data flow graphs)的机器学习库

2. 核心概念

2.1 数据流图(Dataflow Graph)

用节点+有向边描述数学运算的有向无环图。

nodes一般用来表示的各类操作，包括数学运算、数据填充、结果输出、变量读写等操作。每个节点上的操作需要分配到具体的物理设备（CPU/GPU）上执行。

节点	举例
数学函数/表达式	MatMul、BiasAdd、Softmax
存储模型参数的变量（variable）	W、b
占位符（placeholder）	input、label
梯度值	模型参数的梯度Gradients
更新模型参数的操作	Update W、Update b
更新后的模型参数	W、b

edges表示nodes之间的输入/输出关系。edges可以输运tensors(size可动态调整的多维数据数组，即张量)。

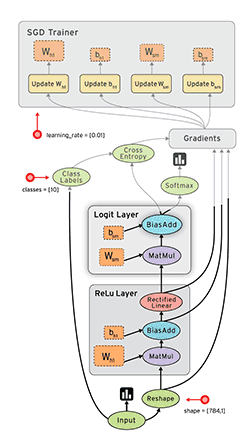
2.1.1 执行原理：DAG拓扑排序

Tips: 节点的执行顺序并不完全依赖于代码中定义的顺序，与节点之间的逻辑关系以及运行时库的实现机制相关。

以节点名称作为关键字、入度作为值，创建一张散列表，将数据流图上的所有节点放入散列表。
为数据流图创建一个可执行节点队列，将散列表中入度为0的节点加入队列，并从散列表中删除此节点。如果存在多个入度为0的节点，同时执行多个OP的运算，提高执行效率。
依次执行队列的每一个节点，成功后将此节点输出执行的节点的入度减1，更新散列表中对应节点的入度。
重复2、3，直到节点队列为空。

2.2 张量

在TensorFlow中，所有在节点之间传递的数据都为Tensor对象(可以看作 n 维的数组)。

两种tensor：Tensor、SparseTensor（减少高维稀疏数据的内存占用）

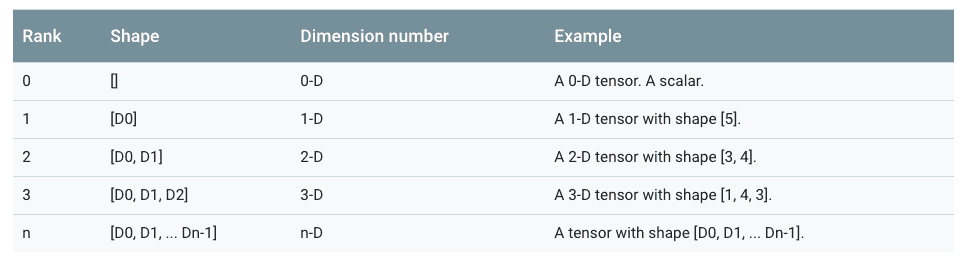
张量的阶（rank）表示数据的最大维度

张量在逻辑定义上是数据载体，在物理实现时是一个句柄，存储张量的元信息+指向数据的内存缓冲区指针，实现内存复用。通过引用计数方式判断是否应该释放张量的内存缓冲区。

2.3 会话

会话用来执行定义好的运算，拥有并管理Tensorflow程序运行时的所有资源，调度&执行节点。

构造阶段完成后, 才能启动图。启动图的第一步是创建Session, 如果无任何创建参数, 会话构造器将启动默认图。

import tensorflow as tf
# 创建数据流图，z=x*y，x、y为数据节点
x = tf.placeholder(tf.float32)
y = tf.placeholder(tf.float32)
z = x * y
sess = tf.Session()
# 求解张量z的值，对数据节点x、y分别填充输入数据
print(sess.run(z, feed_dict={x: 3.0, y: 2.0}))
sess.close()

2.4 优化器

机器学习大致分为3种：监督学习、无监督学习、半监督学习

y_model = tf.mul(X, w)

监督学习：模型、损失函数、优化算法

模型：一系列数学表达式、一组参数

训练本质：在给定的数据上不断拟合，以求出一组在测试数据集使得推理尽可能接近真实值的参数

损失函数：表达模型预测值同真实值差距的函数，用于评估模型的拟合程度

优化算法：使用损失值不断优化模型参数，尽可能减小损失值

最小化损失

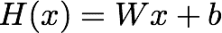
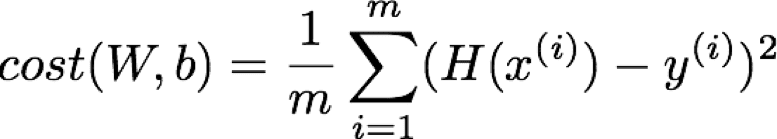
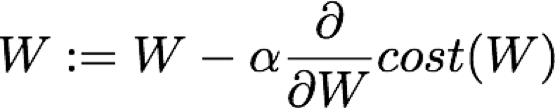
常用优化器
GradientDescentOptimizer
AdagradOptimizer
AdagradDAOptimizer
MomentumOptimizer
AdamOptimizer
FtrlOptimizer
RMSPropOptimizer

继承class tf.train.Optimizer

操作	描述
class tf.train.Optimizer	基本的优化类，该类不常常被直接调用，而较多使用其子类，比如GradientDescentOptimizer, AdagradOptimizer或者MomentumOptimizer
tf.train.Optimizer.init(use_locking, name)	创建一个新的优化器，该优化器必须被其子类(subclasses)的构造函数调用
tf.train.Optimizer.minimize(loss, global_step=None, var_list=None, gate_gradients=1, aggregation_method=None, colocate_gradients_with_ops=False, name=None, grad_loss=None)	添加操作节点，用于最小化loss，并更新var_list该函数是简单的合并了compute_gradients()与apply_gradients()函数返回为一个优化更新后的var_list，如果global_step非None，该操作还会为global_step做自增操作
tf.train.Optimizer.compute_gradients(loss,var_list=None, gate_gradients=1, aggregation_method=None, colocate_gradients_with_ops=False, grad_loss=None)	对var_list中的变量计算loss的梯度该函数为函数minimize()的第一部分，返回一个以元组(gradient, variable)组成的列表
tf.train.Optimizer.apply_gradients(grads_and_vars, global_step=None, name=None)	将计算出的梯度应用到变量上，是函数minimize()的第二部分，返回一个应用指定的梯度的操作Operation，对global_step做自增操作
tf.train.Optimizer.get_name()	获取名称

minimize()合并了compute_gradients()与apply_gradients()

# 创建一个optimizer.
opt = GradientDescentOptimizer(learning_rate=0.1)

# 计算<list of variables>相关的梯度
grads_and_vars = opt.compute_gradients(loss, <list of variables>)

# grads_and_vars为tuples (gradient, variable)组成的列表。
#对梯度进行想要的处理
capped_grads_and_vars = [(MyCapper(gv[0]), gv[1]) for gv in grads_and_vars]

# 令optimizer运用capped的梯度(gradients)
opt.apply_gradients(capped_grads_and_vars)

3. 架构

以C API为界，将整个系统分为「前端」和「后端」两个子系统。

前端系统扮演了Client的角色，完成计算图的构造，通过转发Protobuf格式的GraphDef给后端系统的Master，并启动计算图的执行过程。

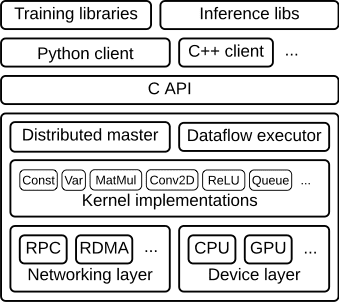
工作流程：构造图、编排图、执行

客户端client

将整个计算过程转义成一个数据流graph，通过session，将graph传递给master执行

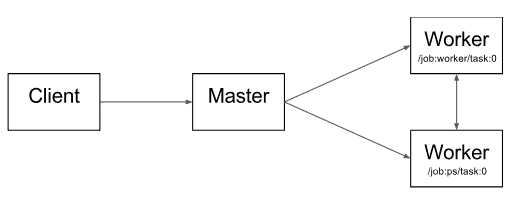
分布式主节点Distributed Master

基于用户传递给Session.run()中的参数来进行修剪整个完整的graph，提取其中特定subgraph；

将上述subgraph划分成不同部分，并将其对应不同的进程和devices中；

将上述划分的部分分布到worker services上；

每个worker services执行其收到的graph块

工作节点的服务Worker Services (one for each task)

使用可用的硬件kernel（如cpu，gpu）计划执行接收到的graph块表示的计算部分；

与其他work services相互发送和接收计算结果

核的实现Kernel Implementations

执行graph操作的计算部分

master使用标准的优化方法去做优化，如公共子表达式消除和常量的绑定。然后给优化后的subgraphs或pieces定义不同的坐标，每个坐标对应了不同的执行设备如”/job:worker/task:0” 和”/job:ps/task:0”

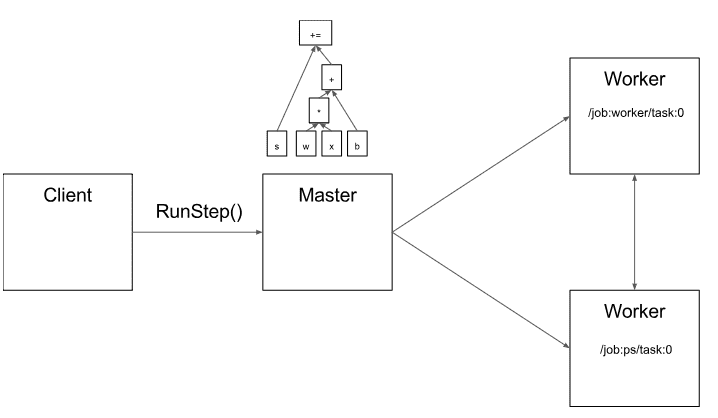
“PS”表示parameter server：一个task负责存储和更新模型的参数，其他worker会发送他们迭代优化的参数给PS。

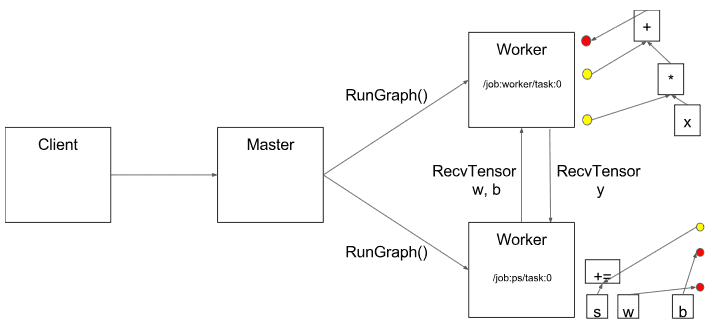
Master 通过调用 RunGraph 接口，通知所有 Worker 执行子图运算。其中，Worker 之间可以通过调用 RecvTensor 接口，完成数据的交换。

4. 可视化

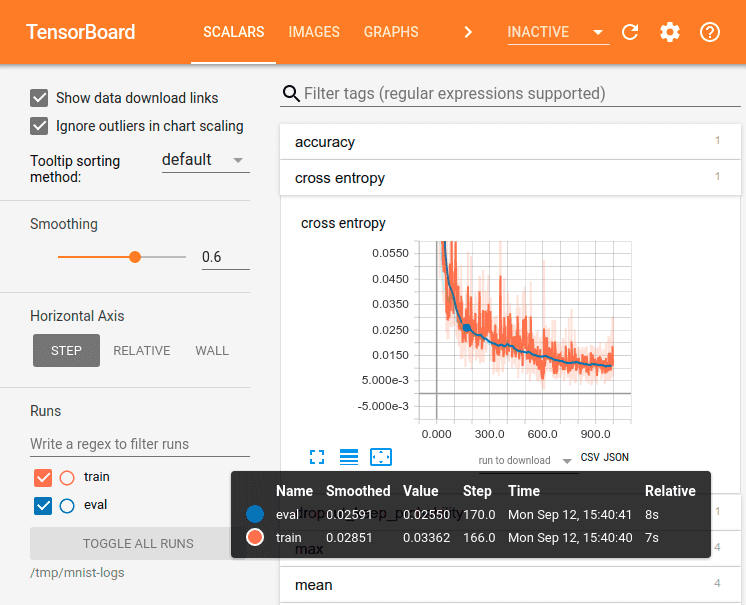
4.1 Tensorboard

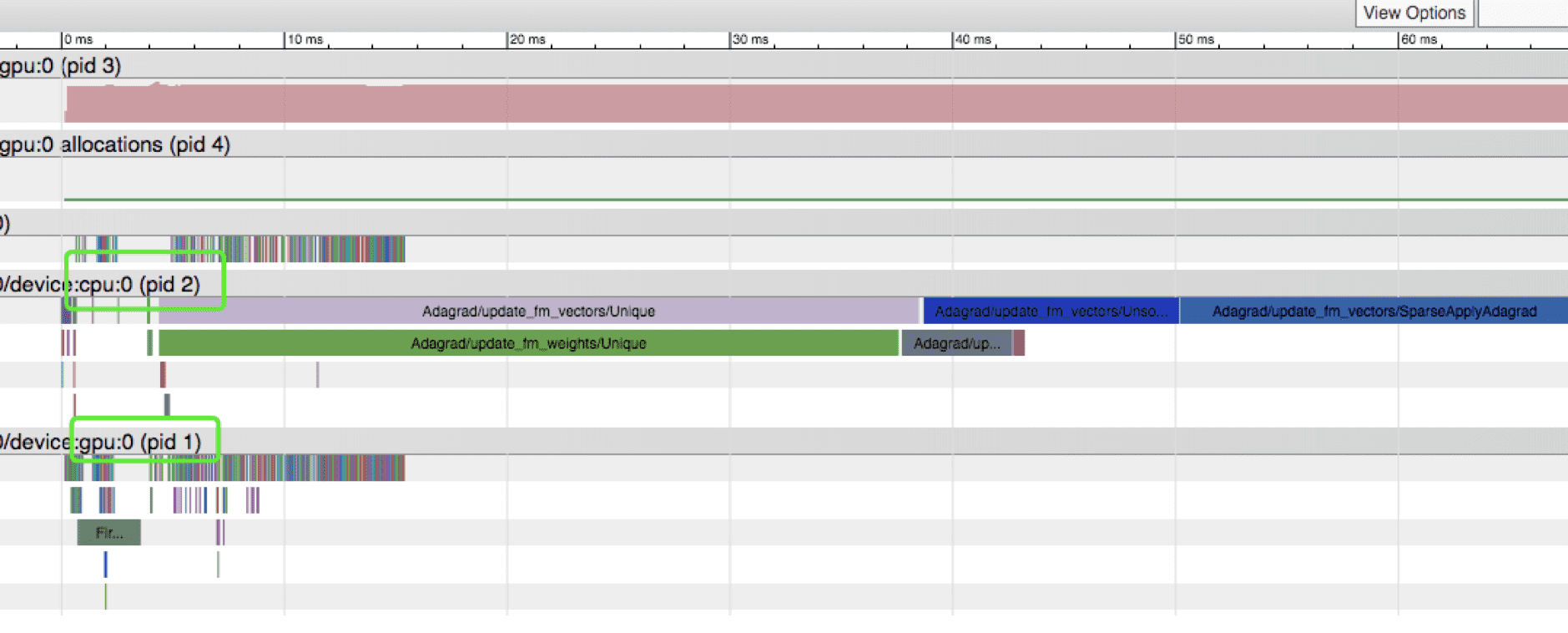
4.2 Profiling

profiler-ui

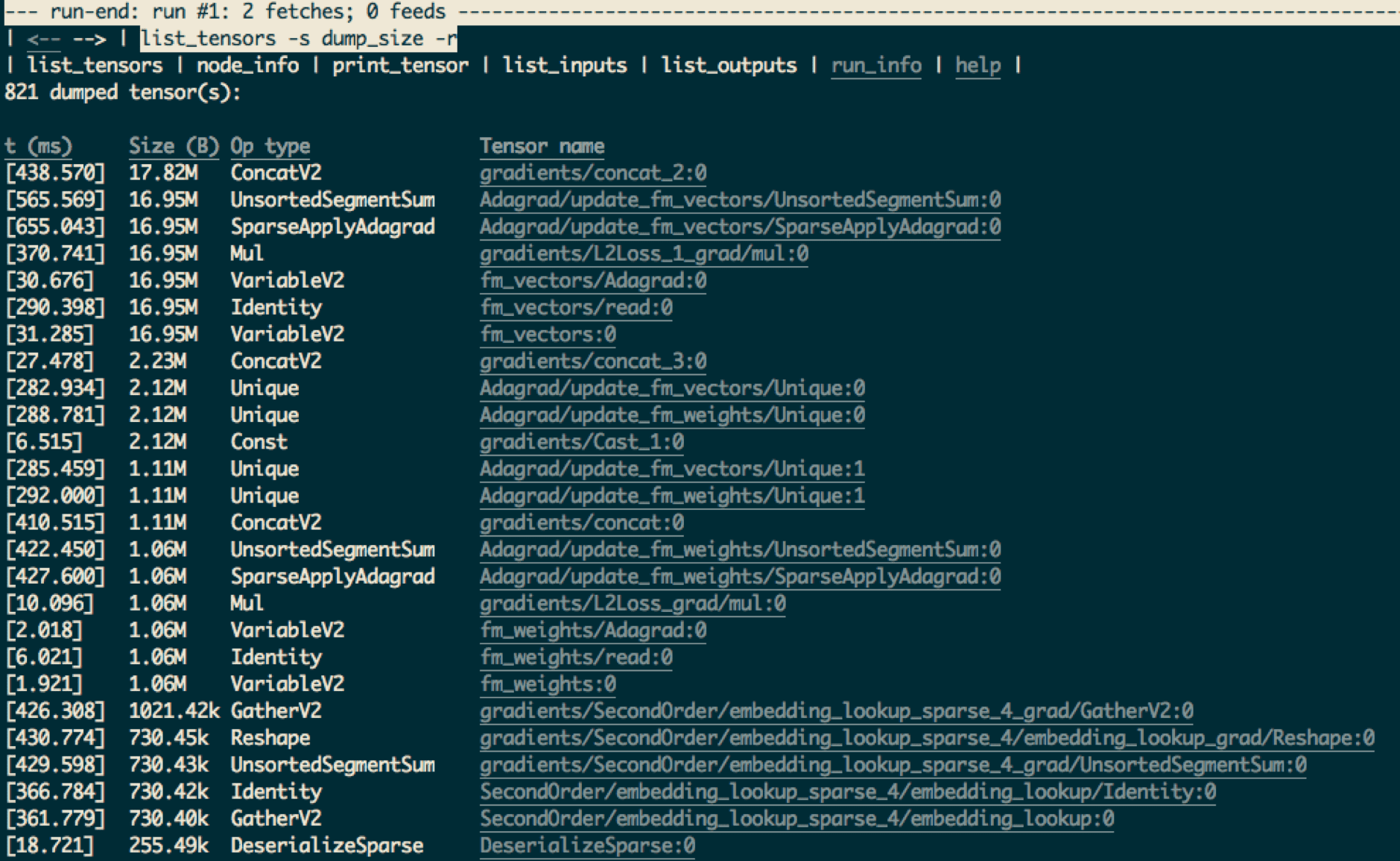
tfdbg

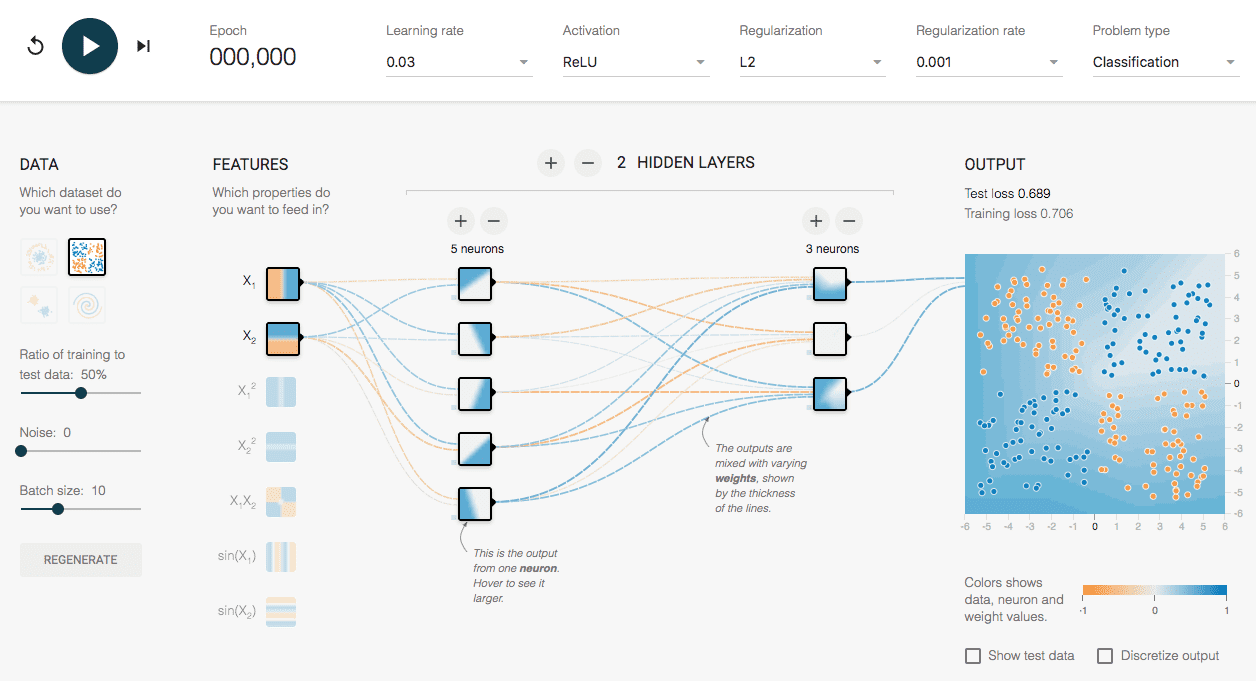
4.3 Playground

http://playground.tensorflow.org

5. 实践

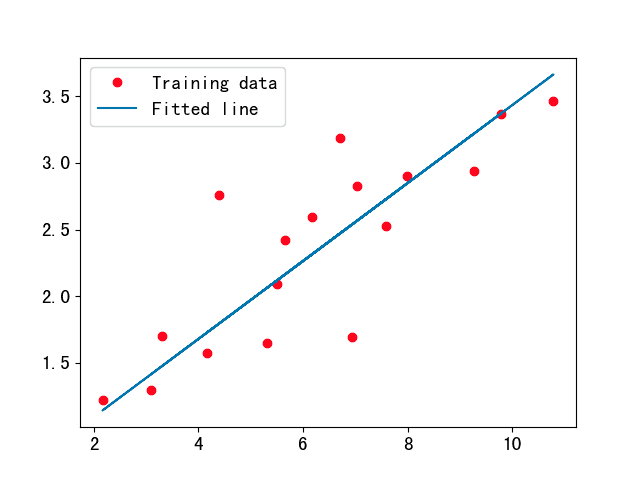
5.1 一元线性回归模型

Y = WX + b = w1x1 + w2x2 + … + wnxn + b

训练过程分为8个步骤：

定义超参数
输入数据
构建模型
定义损失函数
创建优化器
定义单步训练操作
创建会话
迭代训练

import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np

# 打印日志的步长
log_step = 50
# ================ 1.定义超参数 ================
# 学习率
learning_rate = 0.01
# 最大训练步数
max_train_steps = 1000
# ================ 2.输入数据 ================
# 构造训练数据
train_X = np.array([[3.3],[4.4],[5.5],[6.71],[6.93],[4.168],[9.779],[6.182],[7.59],[2.167],[7.042],[10.791],[5.313],[7.997],[5.654],[9.27],[3.1]], dtype=np.float32)
train_Y = np.array([[1.7],[2.76],[2.09],[3.19],[1.694],[1.573],[3.366],[2.596],[2.53],[1.221],[2.827],[3.465],[1.65],[2.904],[2.42],[2.94],[1.3]], dtype=np.float32)
total_samples = train_X.shape[0]
# ================ 3.构建模型 ================
# 输入数据
X = tf.placeholder(tf.float32, [None, 1])
# 模型参数
W = tf.Variable(tf.random_normal([1, 1]), name="weight")
b = tf.Variable(tf.zeros([1]), name="bias")
# 推理值
Y = tf.matmul(X, W) + b
# ================ 4.定义损失函数 ================
# 实际值
Y_ = tf.placeholder(tf.float32, [None, 1])
# 均方差
loss = tf.reduce_sum(tf.pow(Y-Y_, 2))/(2*total_samples)
# ================ 5.创建优化器 ================
# 随机梯度下降优化器
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
# ================ 6.定义单步训练操作 ================
# 最小化损失值
train_op = optimizer.minimize(loss)
# ================ 7.创建会话 ================
with tf.Session() as sess:
    # 初始化全局变量
    sess.run(tf.global_variables_initializer()) 
# ================ 8.迭代训练 ================
    print("Start training:")
    for step in xrange(max_train_steps):
        sess.run(train_op, feed_dict={X: train_X, Y_: train_Y})
        # 每隔log_step步打印一次日志
        if step % log_step == 0:
            c = sess.run(loss, feed_dict={X: train_X, Y_:train_Y})
            print("Step:%d, loss==%.4f, W==%.4f, b==%.4f" % 
                    (step, c, sess.run(W), sess.run(b)))
    # 计算训练完毕的模型在训练集上的损失值，作为指标输出
    final_loss = sess.run(loss, feed_dict={X: train_X, Y_: train_Y})
    # 计算训练完毕的模型参数W和b
    weight, bias = sess.run([W, b])
    print("Step:%d, loss==%.4f, W==%.4f, b==%.4f" % 
            (max_train_steps, final_loss, sess.run(W), sess.run(b)))
    print("Linear Regression Model: Y==%.4f*X+%.4f" % (weight, bias))

输出：
Start training:
Step:0, loss==2.8679, W==0.0054, b==0.0411
Step:50, loss==0.1045, W==0.3457, b==0.1317
Step:100, loss==0.1013, W==0.3402, b==0.1710
Step:150, loss==0.0985, W==0.3350, b==0.2080
Step:200, loss==0.0961, W==0.3301, b==0.2428
Step:250, loss==0.0939, W==0.3254, b==0.2755
Step:300, loss==0.0919, W==0.3211, b==0.3064
Step:350, loss==0.0902, W==0.3170, b==0.3354
Step:400, loss==0.0887, W==0.3131, b==0.3627
Step:450, loss==0.0874, W==0.3095, b==0.3884
Step:500, loss==0.0862, W==0.3061, b==0.4126
Step:550, loss==0.0851, W==0.3029, b==0.4353
Step:600, loss==0.0842, W==0.2999, b==0.4567
Step:650, loss==0.0833, W==0.2970, b==0.4769
Step:700, loss==0.0826, W==0.2944, b==0.4959
Step:750, loss==0.0820, W==0.2918, b==0.5137
Step:800, loss==0.0814, W==0.2895, b==0.5305
Step:850, loss==0.0809, W==0.2872, b==0.5463
Step:900, loss==0.0804, W==0.2851, b==0.5612
Step:950, loss==0.0800, W==0.2832, b==0.5752
Step:1000, loss==0.0797, W==0.2814, b==0.5881
Linear Regression Model: Y==0.2814*X+0.5881

吉吉于

free

Brief introduction to tensorflow

1. 关于Tensorflow

2. 核心概念

2.1 数据流图(Dataflow Graph)

2.1.1 执行原理：DAG拓扑排序

2.2 张量

2.3 会话

2.4 优化器

3. 架构

4. 可视化

4.1 Tensorboard

4.2 Profiling

4.3 Playground

5. 实践

5.1 一元线性回归模型

Brief introduction to tensorflow

1. 关于Tensorflow

2. 核心概念

2.1 数据流图(Dataflow Graph)

2.1.1 执行原理：DAG拓扑排序

2.2 张量

2.3 会话

2.4 优化器

3. 架构

4. 可视化

4.1 Tensorboard

4.2 Profiling

4.3 Playground

5. 实践

5.1 一元线性回归模型

Related Posts