桶排序
04 Nov 2012**桶排序的基本思想 **
** **假设有一组长度为N的待排关键字序列K[1….n]。首先将这个序列划分成M个的子区间(桶) 。然后基于某种映射函数 ,将待排序列的关键字k映射到第i个桶中(即桶数组B的下标 i) ,那么该关键字k就作为B[i]中的元素(每个桶B[i]都是一组大小为N/M的序列)。接着对每个桶B[i]中的所有元素进行比较排序(可以使用快 排)。然后依次枚举输出B[0]….B[M]中的全部内容即是一个有序序列。
**[桶—关键字]映射函数 **
bindex=f(key) 其中,bindex 为桶数组B的下标(即第bindex个桶), k为待排序列的关键字。桶排序之所以能够高效,其关键在于这个映射函数,它必须做到:如果关键字k1<k2,那么f(k1)<=f(k2)。也就是说B(i)中的最小数据都要大于B(i-1)中最大数据。很显然,映射函数的确定与数据本身的特点有很大的关系,我们下面举个例子:
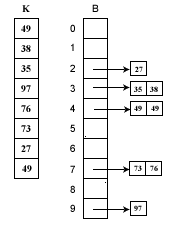
假如待排序列K= {49、 38 、 35、 97 、 76、 73 、 27、 49 }。这些数据全部在1—100之间。因此我们定制10个桶,然后确定映射函数f(k)=k/10。则第一个关键字49将定位到第4个桶中(49/10=4)。依次将所有关键字全部堆入桶中,并在每个非空的桶中进行快速排序后得到如下图所示:
**桶排序代价分析 **
桶排序利用函数的映射关系,减少了几乎所有的比较工作。实际上,桶排序的f(k)值的计算,其作用就相当于快排中划分,已经把大量数据分割成了基本有序的数据块(桶)。然后只需要对桶中的少量数据做先进的比较排序即可。
对N个关键字进行桶排序的时间复杂度分为两个部分:
(1) 循环计算每个关键字的桶映射函数,这个时间复杂度是O(N)。
(2) 利用先进的比较排序算法对每个桶内的所有数据进行排序,其时间复杂度为 ∑ O(Ni*logNi) 。其中Ni 为第i个桶的数据量。
很显然,第(2)部分是桶排序性能好坏的决定因素。尽量减少桶内数据的数量是提高效率的唯一办法(因为基于比较排序的最好平均时间复杂度只能达到O(N*logN)了)。因此,我们需要尽量做到下面两点:
(1) 映射函数f(k)能够将N个数据平均的分配到M个桶中,这样每个桶就有[N/M]个数据量。
(2) 尽量的增大桶的数量。极限情况下每个桶只能得到一个数据,这样就完全避开了桶内数据的”比较”排序操作。 当然,做到这一点很不容易,数据量巨大的情况下,f(k)函数会使得桶集合的数量巨大,空间浪费严重。这就是一个时间代价和空间代价的权衡问题了。
对于N个待排数据,M个桶,平均每个桶[N/M]个数据的桶排序平均时间复杂度为:
O(N)+O(M*(N/M)*log(N/M))=O(N+N*(logN-logM))=O(N+N*logN-N*logM)
当N=M时,即极限情况下每个桶只有一个数据时。桶排序的最好效率能够达到O(N)。
总结: 桶排序的平均时间复杂度为线性的O(N+C),其中C=N*(logN-logM)。如果相对于同样的N,桶数量M越大,其效率越高,最好的时间复杂度达到O(N)。 当然桶排序的空间复杂度 为O(N+M),如果输入数据非常庞大,而桶的数量也非常多,则空间代价无疑是昂贵的。此外,桶排序是稳定的。
以上转载自:http://hxraid.iteye.com/blog/647759
#include <stdio.h>
void swap(int *a, int *b)
{
int temp = *a;
*a = *b;
*b = temp;
}
int partition(int *array, int low, int high)
{
int middle = (low + high)/2;
for(int i=low,j=high; i<j; ) {
while(array[i] < array[middle]) ++i;
if(i < j && i != middle) {
swap(&array[i], &array[middle]);
middle = i;
}
while(array[j] > array[middle]) --j;
if(i < j && j != middle) {
swap(&array[j], &array[middle]);
middle = j;
}
}
return middle;
}
int quicksort(int *array, int low, int high)
{
int piovt_pos;
if(low < high) {
piovt_pos = partition(array, low, high);
quicksort(array, low, piovt_pos - 1);
quicksort(array, piovt_pos + 1, high);
}
}
struct barrel {
int a[10];
int count;
};
int main()
{
int data[] = {23, 12, 3, 54, 1, 98, 24, 34};
int min = data[0];
int max = data[0];
for(int i=1; i<sizeof(data)/sizeof(int); ++i) {
min = min < data[i] ? min : data[i];
max = max > data[i] ? max : data[i];
}
int num = (max - min + 1)/10 + 1;
barrel *pBarrel = new barrel[num];
for(int i=0; i<sizeof(data)/sizeof(int); ++i) {
int j = (pBarrel+((data[i]-min+1)/10))->count;
(pBarrel+((data[i]-min+1)/10))->a[j] = data[i];
(pBarrel+((data[i]-min+1)/10))->count++;
}
static int pos = 0;
for(int i=0; i<num; ++i) {
quicksort((pBarrel+i)->a, 0, (pBarrel+i)->count-1);
for(int j=0; j<(pBarrel+i)->count; ++j) {
data[pos++] = (pBarrel+i)->a[j];
}
}
for(int i=0; i<8; ++i) {
printf("%d ", data[i]);
}
return 0;
}