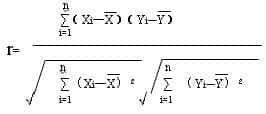前言：

很早就想做一个像豆瓣电台那样的个性化音乐推荐系统，去年写了一些，后来不了了之，对数据挖掘没有太多的了解，总是抱怨时间不够用，今天开始强迫学习一些相关知识，争取一年内做出来一个perfect的推荐系统，此文为记。

从基本的零碎的概念说起吧，慢慢积累一些有用的知识，来吧~

欧几里德距离

欧几里得距离定义： 欧几里得距离（ Euclidean distance）也称欧式距离，它是一个通常采用的距离定义，它是在m维空间中两个点之间的真实距离。

在二维和三维空间中的欧式距离的就是两点之间的距离，二维的公式是

d = sqrt((x1-x2)^+(y1-y2)^)

三维的公式是

d=sqrt((x1-x2)^+(y1-y2)^+(z1-z2)^)

推广到n维空间，欧式距离的公式是

d=sqrt( ∑(xi1-xi2)^ ) 这里i=1,2..n

xi1表示第一个点的第i维坐标,xi2表示第二个点的第i维坐标

n维欧氏空间是一个点集,它的每个点可以表示为(x(1),x(2),…x(n)),其中x(i)(i=1,2…n)是实数,称为x的第i个坐标,两个点x和y=(y(1),y(2)…y(n))之间的距离d(x,y)定义为上面的公式.

欧氏距离看作信号的相似程度。 距离越近就越相似，就越容易相互干扰，误码率就越高。

**皮尔逊相关系数
**

皮尔逊相关系数又称为简单相关系数，英文名称：pearson correlation coefficient，它描述了两个定距变量间联系的紧密程度（线性关系）。

按照大学的线性数学水平来理解, 可以看做是两组数据的向量夹角的余弦.

皮尔逊相关系数是一种度量两个变量间相关程度的方法。它是一个介于 1 和 -1 之间的值，其中，1 表示变量完全正相关， 0 表示无关，-1 表示完全负相关。

R的取值在-1与+1之间，若R＞0，表明两个变量是正相关，即一个变量的值越大，另一个变量的值也会越大；若R＜0，表明两个变量是负相关，即一个变量的值越大另一个变量的值反而会越小。R的绝对值越大表明相关性越强，要注意的是这里并不存在因果关系。若R=0，表明两个变量间不是线性相关，但有可能是其他方式的相关（比如曲线方式）。

计算公式：

---

下面我们用一组用户对电影评分的数据来具体分析一下：

欧几里得距离（d）越小，皮尔逊相关系数（r）越大，两个用户兴趣越相投。

我们规定均以结果越大表示两人兴趣越相近，则d=1/(1+d)，而且可以避免被0除。

以下代码均以python为准，简洁方便~

critics={'Lisa Rose': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.5,
 'Just My Luck': 3.0, 'Superman Returns': 3.5, 'You, Me and Dupree': 2.5, 
 'The Night Listener': 3.0},
'Gene Seymour': {'Lady in the Water': 3.0, 'Snakes on a Plane': 3.5, 
 'Just My Luck': 1.5, 'Superman Returns': 5.0, 'The Night Listener': 3.0, 
 'You, Me and Dupree': 3.5}, 
'Michael Phillips': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.0,
 'Superman Returns': 3.5, 'The Night Listener': 4.0},
'Claudia Puig': {'Snakes on a Plane': 3.5, 'Just My Luck': 3.0,
 'The Night Listener': 4.5, 'Superman Returns': 4.0, 
 'You, Me and Dupree': 2.5},
'Mick LaSalle': {'Lady in the Water': 3.0, 'Snakes on a Plane': 4.0, 
 'Just My Luck': 2.0, 'Superman Returns': 3.0, 'The Night Listener': 3.0,
 'You, Me and Dupree': 2.0}, 
'Jack Matthews': {'Lady in the Water': 3.0, 'Snakes on a Plane': 4.0,
 'The Night Listener': 3.0, 'Superman Returns': 5.0, 'You, Me and Dupree': 3.5},
'Toby': {'Snakes on a Plane':4.5,'You, Me and Dupree':1.0,'Superman Returns':4.0}}

保存为recommendation.py

下面我们在recommendation.py中添加计算欧几里得距离的公式：

from math import sqrt

# Returns a distance-based similarity score for person1 and person2
def sim_distance(prefs, person1, person2):

  # Get the list of shared_items
  si = {}
  for item in prefs[person1]:
    if item in prefs[person2]:
      si[item] = 1

  # if they have no ratings in common, return 0
  if len(si) == 0: 
    return 0 

  # Add up the squares of all the differences
  sum_of_squares=sum([pow(prefs[person1][item]-prefs[person2][item],2) 
                      for item in prefs[person1] if item in prefs[person2]])

  return 1/(1+sqrt(sum_of_squares))

保存，执行函数:

reload(recommendation)

<module ‘recommendation’ from ‘recommendation.py’>

recommendation.sim_distance(recommendation.critics,’Lisa Rose’,’Gene Seymour’)
0.29429805508554946

OK,对我来说上边输出的这一串小数是很令人激动的，因为以前在写豆瓣fm桌面版程序时，分析它的api时，就会看到一些如此的小数~

比如打开http://douban.fm/j/mine/playlist?type=n&channel=1

服务器会返回：

{“r”:0,”song”:[{“picture”:”http:\/\/img3.douban.com\/mpic\/s3839372.jpg”,”albumtitle”:”林忆莲’s”,”company”:”EMI”,”rating_avg”:4.27576,”public_time”:”2000”,”ssid”:”abeb”,”album”:”\/subject\/1468460\/”,”like”:1,”artist”:”林忆莲”,”url”:”http:\/\/mr4.douban.com\/201212021405\/1ea3b5a2361f145a7ac517725d1eb7b6\/view\/song\/small\/p741203.mp3”,”title”:”至少还有你”,”subtype”:””,”length”:274,”sid”:”741203”,”aid”:”1468460”},{“picture”:”http:\/\/img3.douban.com\/mpic\/s3336480.jpg”,”albumtitle”:”寓言”,”company”:”EMI”,”rating_avg”:4.64341,”public_time”:”2000”,”ssid”:”d148”,”album”:”\/subject\/1402531\/”,”like”:0,”artist”:”王菲”,”url”:”http:\/\/mr3.douban.com\/201212021405\/716db9f65f9d90d10e67841dd9d2652f\/view\/song\/small\/p1023377.mp3”,”title”:”笑忘书”,”subtype”:””,”length”:267,”sid”:”1023377”,”aid”:”1402531”},{“picture”:”http:\/\/img3.douban.com\/mpic\/s3714698.jpg”,”albumtitle”:”城堡”,”company”:”Sony”,”rating_avg”:3.74095,”public_time”:”2004”,”ssid”:”56be”,”album”:”\/subject\/1405483\/”,”like”:0,”artist”:”蔡依林”,”url”:”http:\/\/mr4.douban.com\/201212021405\/7c92e86625326ccba99781a52ba8b4ee\/view\/song\/small\/p473552.mp3”,”title”:”倒带”,”subtype”:””,”length”:266,”sid”:”473552”,”aid”:”1405483”},{“picture”:”http:\/\/img3.douban.com\/mpic\/s1443620.jpg”,”albumtitle”:”周蕙精选”,”company”:”福茂”,”rating_avg”:4.04986,”public_time”:”1999”,”ssid”:”46f6”,”album”:”\/subject\/1405009\/”,”like”:0,”artist”:”周蕙”,”url”:”http:\/\/mr4.douban.com\/201212021405\/c495214e12e05a47da353006132de036\/view\/song\/small\/p674182.mp3”,”title”:”约定”,”subtype”:””,”length”:260,”sid”:”674182”,”aid”:”1405009”},{“picture”:”http:\/\/img3.douban.com\/mpic\/s1498586.jpg”,”albumtitle”:”风中有朵雨做的云”,”company”:”Sony”,”rating_avg”:4.22522,”public_time”:”1993”,”ssid”:”1e15”,”album”:”\/subject\/1480936\/”,”like”:0,”artist”:”孟庭苇”,”url”:”http:\/\/mr5.douban.com\/201212021405\/4c7719b3d34c2296bb56bf9a891008c3\/view\/song\/small\/p184451.mp3”,”title”:”风中有朵雨做的云”,”subtype”:””,”length”:263,”sid”:”184451”,”aid”:”1480936”},{“picture”:”http:\/\/img3.douban.com\/mpic\/s3973482.jpg”,”albumtitle”:”北上列车”,”company”:”EMI”,”rating_avg”:4.26843,”public_time”:”2009”,”ssid”:”57c7”,”album”:”\/subject\/4061669\/”,”like”:0,”artist”:”纵贯线”,”url”:”http:\/\/mr4.douban.com\/201212021405\/60d7b5b2f2bdd035bb3e0417a56a58b2\/view\/song\/small\/p1467572.mp3”,”title”:”纵贯线兄弟姐妹”,”subtype”:””,”length”:258,”sid”:”1467572”,”aid”:”4061669”},{“picture”:”http:\/\/img3.douban.com\/mpic\/s3464707.jpg”,”albumtitle”:”陌生人”,”company”:”EMI”,”rating_avg”:4.33905,”public_time”:”2003”,”ssid”:”fef0”,”album”:”\/subject\/1408650\/”,”like”:0,”artist”:”蔡健雅”,”url”:”http:\/\/mr4.douban.com\/201212021405\/cc2afbe9247721355e0007b9c6b696df\/view\/song\/small\/p1022892.mp3”,”title”:”陌生人”,”subtype”:””,”length”:232,”sid”:”1022892”,”aid”:”1408650”},{“picture”:”http:\/\/img3.douban.com\/view\/dale-online\/dale_ad\/public\/e129ce366016979.jpg”,”albumtitle”:”豆瓣FM”,”adtype”:3,”album”:”http:\/\/erebor.douban.com\/redirect\/?ad=11623&uid=56579101&bid=GrKsWFJZx6E&unit=dale_fm_audio&crtr=4%3A1&ns=1354428322710363000&target=http%3A%2F%2Fwww.douban.com%2Fcampaign%2FNescafe_Cafebold%2F”,”like”:”0”,”title”:”雀巢咖啡-敢性咖啡屋”,”url”:”http:\/\/mr3.douban.com\/201212021405\/a2fb6d2455604dcdaff34f132adcff67\/rda\/7f8c61c088041b9.mp3”,”artist”:”雀巢咖啡中国”,”subtype”:”T”,”length”:”15.1”,”sid”:”da11623_80”,”aid”:”82211623”},{“picture”:”http:\/\/img3.douban.com\/mpic\/s4717986.jpg”,”albumtitle”:”失业情歌”,”company”:”金牌大风”,”rating_avg”:3.18664,”public_time”:”2009”,”ssid”:”2fdd”,”album”:”\/subject\/4164404\/”,”like”:0,”artist”:”胡彦斌”,”url”:”http:\/\/mr3.douban.com\/201212021405\/fe10293e264fe925ef18732a5359c468\/view\/song\/small\/p1451797.mp3”,”title”:”父亲”,”subtype”:””,”length”:222,”sid”:”1451797”,”aid”:”4164404”},{“picture”:”http:\/\/img3.douban.com\/mpic\/s3326673.jpg”,”albumtitle”:”至上励合:降临(炫…”,”company”:”天娱传媒”,”rating_avg”:3.4377,”public_time”:”2008”,”ssid”:”8d90”,”album”:”\/subject\/3268371\/”,”like”:0,”artist”:”至上励合”,”url”:”http:\/\/mr3.douban.com\/201212021405\/a312cb9741f143c8fbc6f9156740f010\/view\/song\/small\/p1456768.mp3”,”title”:”小丑”,”subtype”:””,”length”:278,”sid”:”1456768”,”aid”:”3268371”}]}

其中的rating_avg”:4.27576″ 就是平均收听率

下边来编写皮尔逊相关系数：

在recommendation.py继续添加函数：

def sim_pearson(prefs, p1, p2):
  #Get the list of mutually rated shared_items
  si = {}
  for item in prefs[p1]:
    if item in prefs[p2]:
      si[item] = 1

  # if they are no ratings in common, return 0
  if len(si) == 0:
    return 0

  n = len(si)

  # Sums of all the preferences
  sum1 = sum([prefs[p1][it] for it in si])
  sum2 = sum([prefs[p2][it] for it in si])

  # Sums of the squares
  sum1Sq = sum([pow(prefs[p1][it],2) for it in si])
  sum2Sq = sum([pow(prefs[p2][it],2) for it in si])

  # Sums of the products
  pSum = sum([prefs[p1][it]*prefs[p2][it] for it in si])

  # Calculate r (Pearson score)
  num = pSum - (sum1*sum2/n)
  den = sqrt((sum1Sq-pow(sum1,2)/n)*(sum2Sq-pow(sum2,2)/n))
  if den == 0:
    return 0

  r = num / den
  return r

运行如下：

reload(recommendation)

<module ‘recommendation’ from ‘recommendation.py’>

recommendation.sim_pearson(recommendation.critics,’Lisa Rose’,’Gene Seymour’)
0.39605901719066977

ok，后边还有一些东西，下节再写~

转载请注明：于哲的博客 » 欧几里德距离和皮尔逊相关系数