Morris Traversal方法遍历二叉树(非递归,不用栈,O(1)空间)
09 Jul 2013本文主要解决一个问题,如何实现二叉树的前中后序遍历,有两个要求:
- O(1)空间复杂度,即只能使用常数空间;
- 二叉树的形状不能被破坏(中间过程允许改变其形状)。
通常,实现二叉树的前序(preorder)、中序(inorder)、后序(postorder)遍历有两个常用的方法:一是递归(recursive),二是使用栈实现的迭代版本(stack+iterative)。这两种方法都是O(n)的空间复杂度(递归本身占用stack空间或者用户自定义的stack),所以不满足要求。(用这两种方法实现的中序遍历实现可以参考这里。)
Morris Traversal方法可以做到这两点,与前两种方法的不同在于该方法只需要O(1)空间,而且同样可以在O(n)时间内完成。
要使用O(1)空间进行遍历,最大的难点在于,遍历到子节点的时候怎样重新返回到父节点(假设节点中没有指向父节点的p指针),由于不能用栈作为辅助空间。为了解决这个问题,Morris方法用到了线索二叉树(threaded binary tree)的概念。在Morris方法中不需要为每个节点额外分配指针指向其前驱(predecessor)和后继节点(successor),只需要利用叶子节点中的左右空指针指向某种顺序遍历下的前驱节点或后继节点就可以了。
Morris只提供了中序遍历的方法,在中序遍历的基础上稍加修改可以实现前序,而后续就要再费点心思了。所以先从中序开始介绍。
首先定义在这篇文章中使用的二叉树节点结构,即由val,left和right组成:
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
步骤:
- 如果当前节点的左孩子为空,则输出当前节点并将其右孩子作为当前节点。
- 如果当前节点的左孩子不为空,在当前节点的左子树中找到当前节点在中序遍历下的前驱节点。
a) 如果前驱节点的右孩子为空,将它的右孩子设置为当前节点。当前节点更新为当前节点的左孩子。
b) 如果前驱节点的右孩子为当前节点,将它的右孩子重新设为空(恢复树的形状)。输出当前节点。当前节点更新为当前节点的右孩子。
- 重复以上1、2直到当前节点为空。
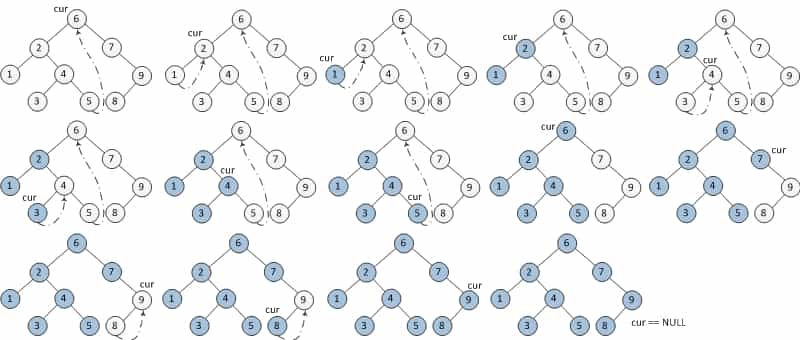
图示:
下图为每一步迭代的结果(从左至右,从上到下),cur代表当前节点,深色节点表示该节点已输出。
代码:
void inorderMorrisTraversal(TreeNode *root) {
TreeNode *cur = root, *prev = NULL;
while (cur != NULL)
{
if (cur->left == NULL) // 1.
{
printf("%d ", cur->val);
cur = cur->right;
}
else
{
// find predecessor
prev = cur->left;
while (prev->right != NULL && prev->right != cur)
prev = prev->right;
if (prev->right == NULL) // 2.a)
{
prev->right = cur;
cur = cur->left;
}
else // 2.b)
{
prev->right = NULL;
printf("%d ", cur->val);
cur = cur->right;
}
}
}
}
前序,后续看原文