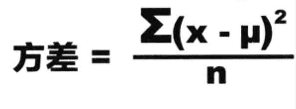标题有点不明觉厉，其实说白了就是全距，四分位数，方差，标准差，以及标准分在实际中的应用。

数据的变异性（散布，离散度）可看作是对不同数值间的差异性的度量。

反映数据变异性的常用指标有极差、标准差和方差。

全距可以用来度量数据集分散程度。

下边分别细说一下。

1.全距

2.四分位数以及n分位数

为了忽略全距里的异常值，我们需要截取中间的一段来分析。

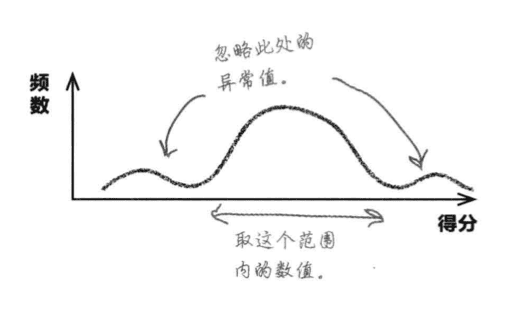
四分位数（Quartile），即统计学中，把所有数值由小到大排列并分成四等份，处于三个分割点位置的得分就是四分位数。

这里的Q1，Q2，Q3就是四分位数。

最小的四分位数，Q1称为下四分位数或者第一四分位数。

最大的四分位数，Q3称为上四分位数或第三四分位数。

中间的四分位数，Q2即中位数。

每两个四分位数之间的距被称为四分位距。

四分位距 = 上四分位数 – 下四分位数

四分位距的优点是：与全距相比，较少受到异常值的影响。

可以类比n分位距~

计算方法：

求下四分位数

1.首先计算n/4

2.如果结果为整数，则下四分位数位于 n/4 这个位置与下一个位置的中间，取这两个位置上的数值的平均值，即得到下四分位数。

3.如果 n/4 不是整数，则想上取整，所得结果即为下四分位数的位置。

举例：

如果有六个数，首先计算6/4 ，得1.5，向上取整得到2，表示下四分位数位置为2。

求上四分位数

1.首先计算3n/4

2.如果结果为整数，则上四分位数位于3n/4这个位置与下一个位置的中间，将这两个位置上的数加起来，然后除以2

3.如果3n/4不是整数，则向上取整，所得到的数字即为上四分位数的位置。

 

3.方差

方差是度量数据分散性的一种方法，是数值与均值的距离的平方数的平均值。

在概率论和数理统计中，方差（英文Variance）用来度量随机变量和其数学期望（即均值）之间的偏离程度。

在许多实际问题中，研究随机变量和均值之间的偏离程度有着很重要的意义。

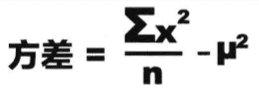
4.标准差

标准差（Standard Deviation） ，中文环境中又常称均方差，但不同于均方误差（mean squared error），

均方误差是各数据偏离平均数的距离平方的平均数，也即误差平方和的平均数，

计算公式形式上接近方差，它的开方叫均方根误差，均方根误差才和标准差形式上接近，

标准差是离均差平方和平均后的方根，用σ表示。

标准差是方差的算术平方根。

标准差能反映一个数据集的离散程度。

平均数相同的，标准差未必相同。

 

 

5.标准分

标准分是一种由原始分推导出来的相对地位量数，它是用来说明原始分在所属的那批分数中 的相对位置的。

求法如下：

Z=(X-X_bar)/S

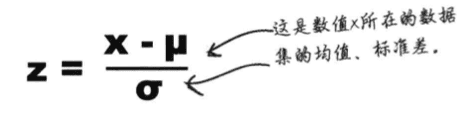
式中，X为原始分数，X_bar为原始分的平均数，S为原始分的标准差。

Z分数是以一批分数的平均数作为参照点，以标准差作为单位表示距离的。

它由正负号和绝 对数值两部分组成，正负号说明原始分是大于还是小于平均数，绝对数值说明原始分距离平 均分数的远近程度。

一批分数全部转换成Z分数后，它们的整个分布形态并没有发生改变。

Z 分数准确地刻划了一个分数在一批分数中的相对位置，但是，由于Z分数有负值，常带有小 数，不易被人理解和应用。

因此人们在Z分数的基础上进一步转换，从而发展起了一系列其 他形式的标准分。

转换通式为：

Z′=αZ+β

式中，Z′为其他形式的标准分，α为基准分，一般等于原始分的平均分X_bar，β是扩大系数，一般等于原始数据的标准差S。

性质：

⑴平均值为0，标准差为1；

⑵分数之间等距，可以作加减运算；

⑶原始分转换为标准分是线性转换，不会改变原始分的分布形状，也不改变原来分数的位置次序。 

6.变异系数

变异系数 (coefficient of variation，CV)：标准差对均值的百分比。

由于标准差的单位和数据值的单位相同，若想比较两组不同单位的数据的变异性大小，就无法直接比较其标准差了。

但若使用变异系数，得到的是无单位的百分比，就可以让不同的数据组相互比较。

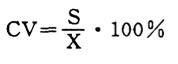
转载请注明：于哲的博客 » 【统计学】分散性与变异性的度量