【统计学】概率计算
12 Nov 2013我这是又回到大一的节奏啊,为了丰富一下空乏的大脑看看统计学,又看到了概率这一章。
这尼玛就是概率论的东西啊,蛋疼,就当复习考研了。
我是个大水逼,下边跟我过一遍概念吧,哈哈哈哈。
1.概率
概率,又称或然率、机会率或机率、可能性,是数学概率论的基本概念,是一个在0到1之间的实数,是对随机事件发生的可能性的度量。
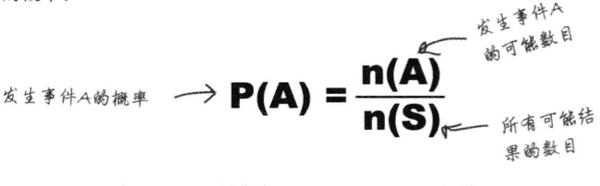
表示一个事件发生的可能性大小的数,叫做该事件的概率。它是随机事件出现的可能性的量度,同时也是概率论最基本的概念之一。
2.维恩图
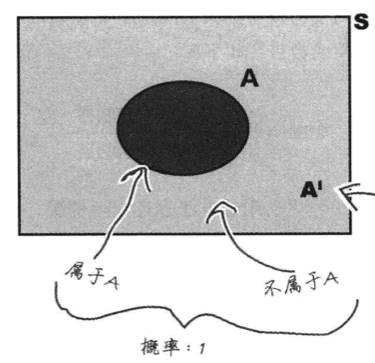
用封闭曲线(内部区域)表示集合及其关系的图形。(Venn Diagram,也称韦恩图)
就是下边这货啦。高中就看够了。
3.对立事件
亦称”逆事件”,不可能同时发生。
若A交B为不可能事件,A并B为必然事件,那么称A事件与事件B互为对立事件,其含义是:事件A一个发生。
定义:其中必有一个发生的两个互斥事件叫做对立事件。
对立事件概率之间的关系:
P(A)+P(B)=1
4.互斥事件
事件A和B的交集为空,A与B就是互斥事件,也叫互不相容事件。
也可叙述为:不可能同时发生的事件。
如A∩B为不可能事件(A∩B=Φ),那么称事件A与事件B互斥,其含义是:事件A与事件B在任何一次试验中不会同时发生
5.条件概率
在同一个样本空间 Ω 中的事件或者子集 A 与 B,如果随机从 Ω 中选出的一个元素属于 B,那么下一个随机选择的元素属于 A 的概率就定义为在 B 的前提下 A 的条件概率。
当且仅当两个随机事件 A 与 B 满足 P(A∩B)=P(A)P(B).的时候,它们才是相互独立的,这样联合概率可以表示为各自概率的简单乘积。
| 同样,对于两个独立事件 A 与 B 有P(A | B) = P(A)以及P(B | A) = P(B)换句话说,如果 A 与 B 是相互独立的,那么 A 在 B 这个前提下的条件概率就是 A 自身的概率; |
同样,B 在 A 的前提下的条件概率就是 B 自身的概率。
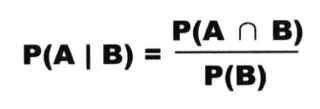
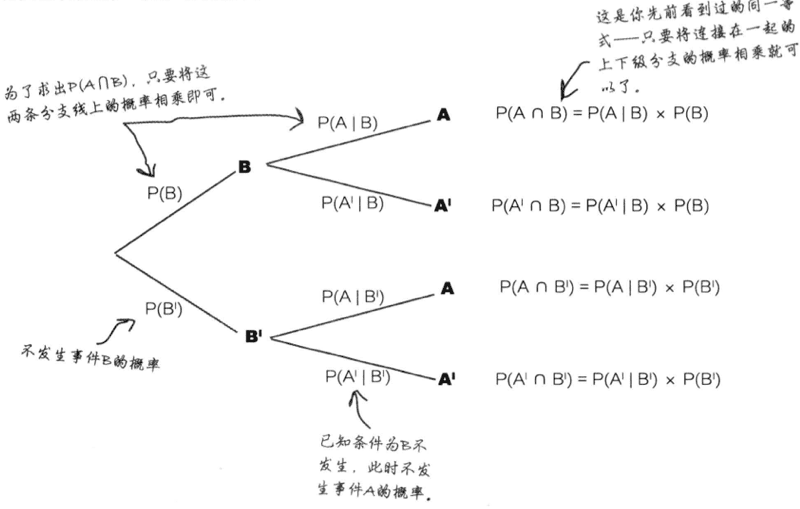
6.概率树
概率树可以帮助你以图形的方式表示概率,也可以计算概率。
7.全概率公式
设实验E的样本空间为S,B1,B2,…,Bn为S的一个划分,且P(Bi)>0(i=1,2,…,n),则对任一事件A
| P(A)=P(A | B1)*P(B1) + P(A | B2)*P(B2) + … + P(A | Bn)*P(Bn). |
8.贝叶斯公式
| P(A | B)=P(B | A)*P(A)/P(B) |
| 贝叶斯定理由英国数学家贝叶斯 ( Thomas Bayes 1702-1763 ) 发展,用来描述两个条件概率之间的关系,比如 P(A | B) 和 P(B | A)。 |
通常,事件A在事件B(发生)的条件下的概率,与事件B在事件A的条件下的概率是不一样的;然而,这两者是有确定的关系,贝叶斯法则就是这种关系的陈述。
作为一个规范的原理,贝叶斯法则对于所有概率的解释是有效的;
然而,频率主义者和贝叶斯主义者对于在应用中概率如何被赋值有着不同的看法:频率主义者根据随机事件发生的频率,或者总体样本里面的个数来赋值概率;
贝叶斯主义者要根据未知的命题来赋值概率。
一个结果就是,贝叶斯主义者有更多的机会使用贝叶斯法则。
| 数学领域 |
|
|---|
| 工程领域 |
|
|---|
| 其他领域 |
|
|---|
9.相关/独立事件
如果A和B是互斥事件,即如果事件A发生,则事件B不发生。这意味着,A的结果会影响B的结果,于是这二者相关。
与此类似,如果A和B是独立事件,则二者不会互斥。
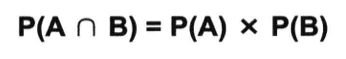
如果上式成立,则A,B相互独立。
11.独立性
| 如果A和B相互独立,则P(A | B) = P(A) |